マクスウェルの方程式(2.1)および式(2.2)を時間及び空間について差分化する際、FDTD法では一次の差分公式が用いられる。もちろん精度をあげるために高次の差分公式を用いた定式化も可能であるが、複雑になるうえに、特に波動を扱う場合には一般に不安定になりやすい。詳しくは示さないが、これはFDTD法に限ったことではなく微分方程式の数値解法一般にいえることである。

　１次差分には前進差分、後進差分および中心差分があるが、図１から明らかなように、中心差分が最も精度の良い差分公式であることから、FDTD法では中心差分が用いられる。なお、これも詳しくは示さないが、前進差分と後進差分での誤差はのオーダー、中心差分ではのオーダーである。

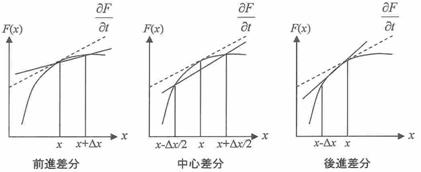
図１　一次差分法のパターン

関数 (ただし、x,y,zは空間、tは時間を表す) において、空間x及び時間tについての中心差分は、

                                 　　　　　　　　　 (2.5)

　　　　　　　　　　　　　　　(2.6)

で与えられる。FDTD法では、先に記述したとおり解析領域を微小セルに分割し、かつ時間も離散化される為、点はそれぞれの係数をとすると、のような各格子点に割り当てられることになる。はセルの各辺の長さでありセルサイズと呼ばれ、は時間ステップという。FDTD法では、を省略して、

　　　　　　　　　　　　　　                       　　　(2.7)

と表記される。

　式(2.7)を用いると式(2.8)、(2.9)は

　　　　　　　　　　　　　             (2.8)

                                          　　　　　　　　　　　　 (2.9)

と書くことができる。