Step,1)において中心差分を用いたことによって、電界と磁界は交互に配置されたことになる。下にその様子を描いた図を示した。

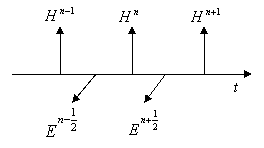
図２　電磁界の時間及び空間配置

今回我々のプログラムでは、図2のように磁界をの整数次の時刻に、電界をの半奇数次の時刻に割り当てることとする。t=nでの磁界をと記すとすると、磁界と電界とからを、ととからを計算する、というように順次、電界・磁界が計算されるが、次にこれを定式化の過程から述べる。

　ここでは例として、波源のない場合を考える。式(2.1),(2.2)をを用いて電界、磁界に直すと、

                                                         (2.10)

　　　　　　　　　　　　　　　　　                  (2.11)

となる。ここで、?、?、?はそれぞれ透磁率、誘電率、導電率であり、場所の関数とする。ただし、今回我々はフォトニックバンドギャップをもつフォトニック結晶を考えているため、導電率?は0とした。よって上の式(2.11)は

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2.11’)

となる。

　式(2.10)左辺の電界に関する時間微分は、磁界の存在する時刻がであることからで行う必要がある。同様に、電界に関する時間微分は、磁界の存在する時刻がであることからで行う必要がある。これをStep1)の表記を用いると、電界・磁界の時間微分はそれぞれ

                                                 (2.12)

　　　　　　　　　　　　　　　　　　　　　         (2.13)

となる。

式(2.12),(2.13)を式(2.10),(2.11’)に代入すると、

                                                (2.14)

　　　　　　　　　　　　　　　　         　       (2.15)

となる。これを、についてまとめると、

                                                 (2.16)

                                                 (2.17)

となる。

　式(2.16)と式(2.17)から分かるように、FDTD法ではの磁界との電界とから次の半ステップ後の磁界が計算され、さらにこの磁界と電界とから次の半ステップ後の電界が計算される。